【2022 NOIP 模拟赛 22】选举 做题记录

Byteland 的选民们要进行总统选举。一共有 $n$ 位选民和 $m$ 位候选人，编号分别从 $1$ 到 $n$ 和从 $1$ 到 $m$ 。

每位选民有一个非空的喜欢的候选人的列表，这个列表是按照喜欢程度排序的。比如说一位选民的列表是 $\{2,4,7\}$ ，那么他最喜欢的候选人是 $2$ 号候选人，次喜欢的是 $4$ 号候选人，再次是 $7$ 号候选人，其余候选人都不喜欢。

选举会进行若干轮，具体规则如下：

• 每一轮，每位选民会投给某位在自己列表中的候选人恰好一票。
• 第一轮，每位选民会投给自己最喜欢的候选人。
• 从第二轮开始，每位选民会投给自己列表中上一轮票数最多的候选人。如果有多位在列表中的候选人票数都是 最多的，那么会投给这些人中最喜欢的那一位（即按照票数为第一关键字，喜欢程度为第二关键字排序）。
• 如果每位选民在第 $i$ 轮 $(i\gt 1)$ 投给的候选人都和在第 $i-1$ 轮投给的候选人一样，那么选举会在第 $i$ 轮结束后停止，并且 random 一位候选人作为总统。

聪明的你一定发现了这个选举没有什么蛋用，但是你只关心选举进行的轮数。

你需要构造出 $n,m$ 和每一位选民的喜欢的候选人的列表，使得最终选举进行的轮数尽可能多。

你还需要保证 $1\le m<n\leq 1000$，所有人的喜欢的候选人的列表大小 $k$ 之和 $\leq 10^5$。

猜测每个点的列表不会很长（因为太长不好构造），那么尝试构造 $k\le 2$ 的答案。这时每个 $k=2$ 的选民都可以看成一条边，候选人则可以看成点，不妨规定每条边出发的点优先级低于指向的点。

不难发现投票的过程相当于是「上一轮最多票的人」不断改变，那么考虑构造一条链，让「上一轮最多票的人」在这条链上一个一个点地跳，先来考虑有 $2$ 个点的情况，显然可以这样构造：（没有出发点的边是 $k=1$ 的选民）

若这样构造「上一轮的票」会这样变化：

$[0,0]\to[3,0]\to[3,0]$

共变化 $3$ 轮。

考虑 $4$ 个点的情况：

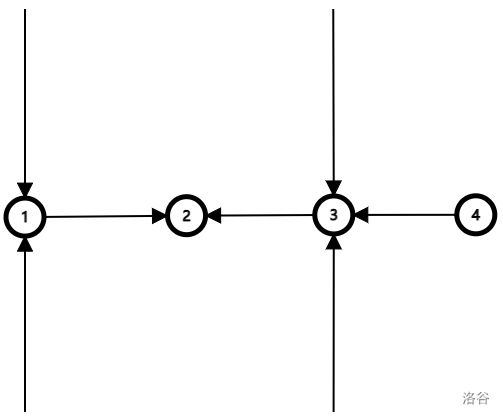
若这样构造「上一轮的票」会这样变化：

$[0,0,0,0]\to[2,2,3,0]\to[2,1,4,0]\to [3,0,4,0]\to [3,0,4,0]$

共变化 $5$ 轮。

不难发现，这样构造刚开始「上一轮的票」是 $[2,2,2,\dots,2,2,3,0]$ 这样的，两轮后变成了 $[2,2,2,\dots,3,0,4,0]$，$3$ 往前移动了两个点，并且后面的点对前面的点和总轮数没有任何影响，所以这样构造的总轮数是 $m+1$。

不难发现，若有 $m$ 个点就会有 $2m-1$ 条边，所以最多可以有 $500$ 个点，总轮数为 $501$，足以通过本题。

代码如下：

#include <iostream>
#include <cstdio>

using namespace std;

int main()
{
	freopen("t.out","w",stdout);
	int k=250-1;
	printf("%d %d\n",k*4+3,(k+1)*2);
	for(int i=1;i<=k;i++)
	{
		printf("1 %d\n",i*2-1);
		printf("1 %d\n",i*2-1);
		printf("2 %d %d\n",i*2,i*2-1);
		printf("2 %d %d\n",i*2,i*2+1);
	}
	printf("1 %d\n",(k+1)*2-1);
	printf("1 %d\n",(k+1)*2-1);
	printf("2 %d %d\n",(k+1)*2-1,(k+1)*2);
	return 0;
}