CF1713D Tournament Countdown 做题记录

这是一道交互题。

有一场由 $2^n$ 位选手组成的锦标赛。

这个锦标赛的规则如下：第 $1$ 位选手与第 $2$ 位选手竞争，第 $3$ 位选手与第 $4$ 位选手竞争……以此类推，比赛结束时会只剩下一位参赛选手，这位参赛选手就是胜利者。

你不知道比赛的结果，但你想通过询问评审团来得知最后谁赢了。

每次询问评审团，你需要给定两个正整数 $a$ 和 $b$，$a$ 和 $b$ 分别代指两位选手的编号。

若 $a$ 选手 比 $b$ 选手 赢的回合更多，评委团将报出数字 $1$；如果 $b$ 选手 比 $a$ 选手 赢的回合更多，评审团将报出数字 $2$；如果这两位选手赢的回合一样多，评审团会报出数字 $0$。

你要做的是在不超过 $\lceil \frac{1}{3} \cdot 2^{n+1} \rceil$ 的次数内找到最后胜利的选手。此处 $\lceil x \rceil$ 表示四舍五入 $x$ 到最近的整数。

这场锦标赛已经过去很久了。所以保证有唯一解。

$1\leq n\leq 17$。

首先显然可以耗费 $2^n-1$ 次询问按照淘汰赛树一层一层询问。

发现 $\left\lfloor\dfrac{2^{n+1}}{3}\right\rfloor=\left\lfloor\dfrac{2}{3}\times 2^n\right\rfloor$，那么考虑用两次询问确定同层相邻四个节点中哪个赢得场数最多。也就是考虑用两次询问从 $[1,2,3,4]$ 中找到下图中被红框框住的节点 $3$：

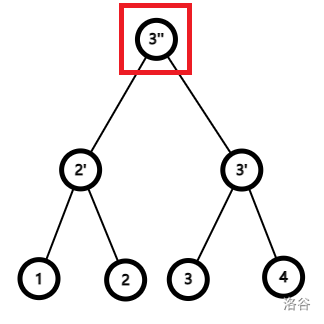
考虑询问 $1,3$：

• 若返回 $1$ 即 $1$ 赢得比 $3$ 多，那么显然 $3$ 和 $2$ 都不可能是赢得最多的，接下来只用询问 $1,4$ 即可找到赢得最多的；
• 若返回 $2$ 即 $3$ 赢得比 $1$ 多，那么类比返回 $1$ 的情况询问 $3,2$ 即可；
• 若返回 $0$ 即赢得一样多，那么显然他们两个都不可能是赢得最多的，接下来询问 $2,4$ 即可。

所以我们每次这样处理一层的节点即可。