做法
最小割。
这是我第一次在赛场上做出有难度的网络流,写篇题解纪念一下。
赛后发现我的建模方法和官方题解并不相同,所以这篇题解也算是提供了一种新奇的建图思路吧。
首先观察到每个人有两种选择:愿意和不愿意。那么可以用源点表示愿意,汇点表示不愿意。具体就是对第 个人建立节点 ,然后从源点向 连一条流量为 的边,从 向汇点连一条流量为 的边:
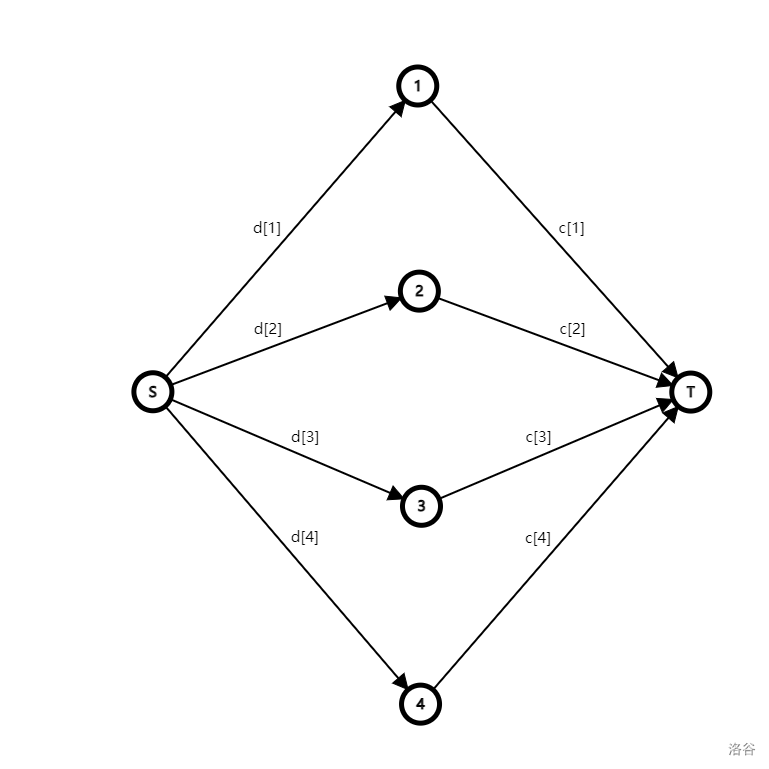
然后考虑同一组内的两个人 意见不同( 选择了愿意)的情况,此时情况如下:
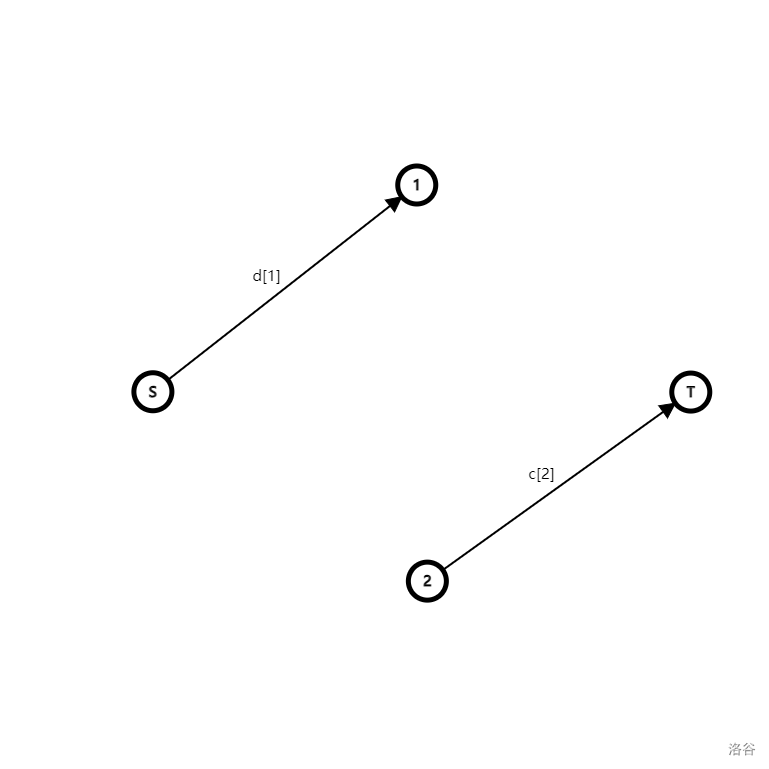
因为会产生 的不满,所以从 向 连一条流量为 的边来增加不满。
对于 选择了愿意但是 选择了不愿意的情况亦然。
加上这些边之后的图如下:(两个奇奇怪怪的点是用来防止边权重叠的)
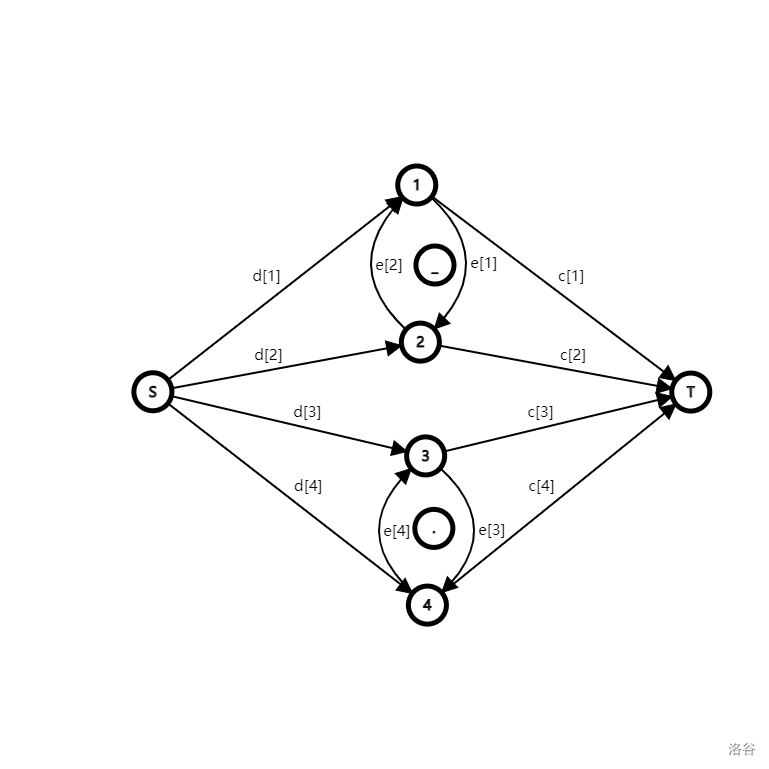
接下来我们就需要解决最棘手的喜欢关系了。(赛场上想了 1h 左右/ll)
首先可以发现,只有一组里两个人都选择愿意才可以合作。所以可以给每一组引入一个点 ,从 分别向两个成员连流量为 的边:
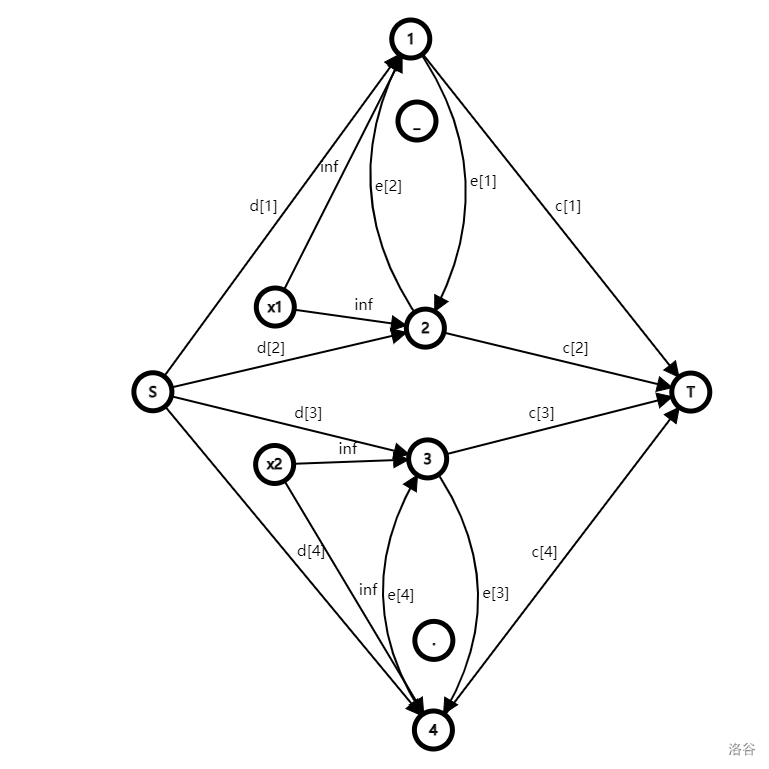
这么连边的目的是,假设有一些流量送到了 :
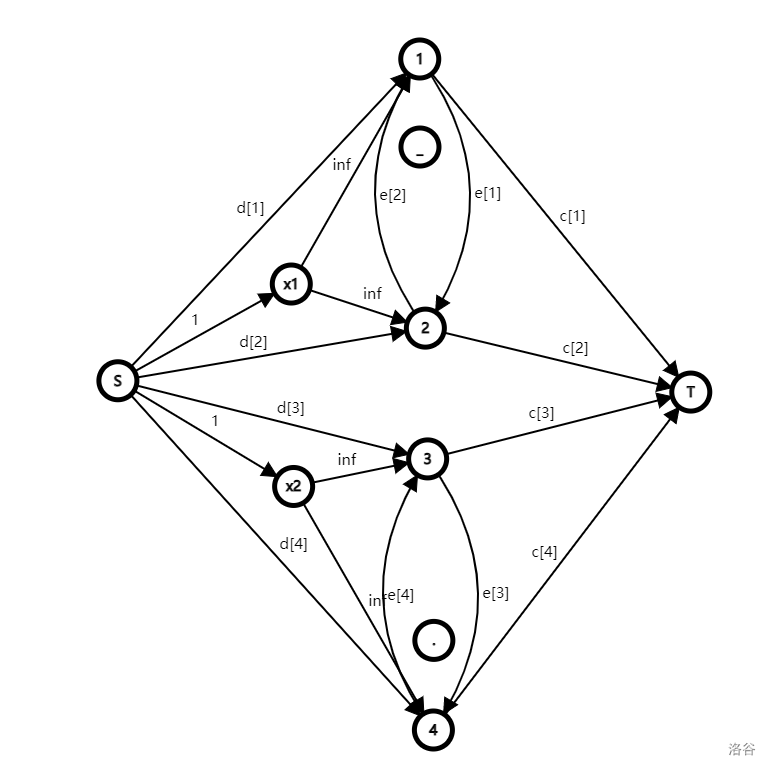
那么就可以保证每一组如果不合作的话给 送流量的边都要被割断,如果合作的话就不隔断,并且如果一组中有一个或以上人选择了不愿意那么就必须不合作。换句话说, 没有流量代表这一组不合作,否则代表这一组合作。
现在我们可以表示合不合作了,接下来考虑喜欢关系的连边。
若第 组关系是 喜欢 ,设 表示 那一组的 , 表示 那一组的 ,那么:
如果 没有和队友合作,并且 选择了愿意,在图上就是 有流量并且 不能有流量。此时会产生 的不满,那么我们可以从有流量的 向不能有流量的 连一条流量为 的边。
如果 选择了不愿意,并且 和队友合作了,在图上就是 连向汇点的边没有被割断并且 有流量。此时会产生 的不满,那么我们可以从有流量的 向可以到达汇点的 连一条流量为 的边。
加上这些边后的图:(假设有一条喜欢关系: 喜欢 )
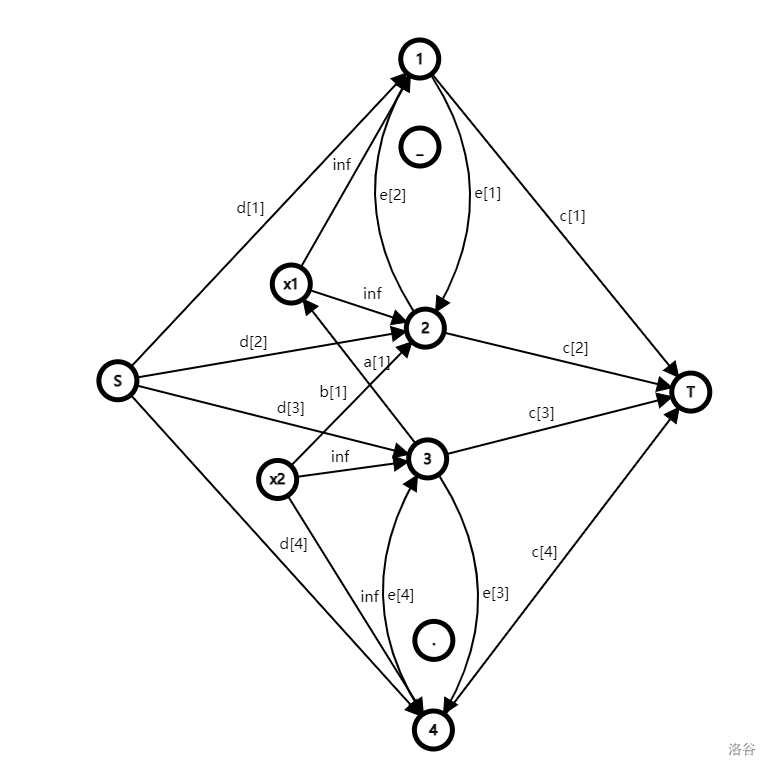
这样我们就建完图了,跑最小割即可。
AC 代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <vector>
#include <map>
#include <set>
using namespace std;
struct node
{
};
typedef long long ll;
const ll S=5000005,MS=1000005;
int n,m,s,t;
int xid[MS];
int esum,to[S],nxt[S],h[MS];
ll c[S];
int dep[MS];
inline void init()
{
esum=1;
memset(h,0,sizeof(h));
s=0;
t=1000003;
}
inline void add(int x,int y,ll w)
{
c[++esum]=w;
to[esum]=y;
nxt[esum]=h[x];
h[x]=esum;
}
inline bool bfs()
{
memset(dep,0,sizeof(dep));
queue<int> q;
q.push(s);
dep[s]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=h[u];i;i=nxt[i])
{
int v=to[i];
if(c[i]>0&&dep[v]==0)
{
dep[v]=dep[u]+1;
q.push(v);
}
}
}
return dep[t]!=0;
}
ll dfs(int u,ll w)
{
if(u==t)
{
return w;
}
ll sum=0;
for(int i=h[u];i;i=nxt[i])
{
int v=to[i];
if(c[i]>0&&dep[v]==dep[u]+1)
{
ll re=dfs(v,min(w,c[i]));
c[i]-=re;
c[i^1]+=re;
sum+=re;
w-=re;
if(w==0)
{
break;
}
}
}
if(sum==0)
{
dep[u]=0;
}
return sum;
}
inline ll dinic()
{
ll ans=0;
while(bfs())
{
ans+=dfs(s,1e17);
}
return ans;
}
inline void slove()
{
scanf("%d%d",&n,&m);
n*=2;
init();
for(int i=1;i<=n;i++)
{
ll C,D,E;
scanf("%lld%lld%lld",&C,&D,&E);
add(s,i,D);
add(i,s,0);
add(i,t,C);
add(t,i,0);
int v=(i&1)?i+1:i-1;
add(i,v,E);
add(v,i,0);
}
for(int i=1;i<=n;i+=2)
{
int u=n+(i+1)/2;
add(u,i,1e17);
add(i,u,0);
add(u,i+1,1e17);
add(i+1,u,0);
xid[i]=u;
xid[i+1]=u;
}
for(int i=1;i<=m;i++)
{
int x,y;
ll a,b;
scanf("%d%d%lld%lld",&x,&y,&a,&b);
int u1=xid[y],v1=xid[x];
add(u1,x,b);
add(x,u1,0);
add(y,v1,a);
add(v1,y,0);
}
printf("%lld\n",dinic());
}
int main()
{
int _=1;
// scanf("%d",&_);
while(_--)
{
slove();
}
return 0;
}