给定长度为 的排列 ,要对于 求出,有多少个长度为 的排列 满足 字典序比 小,且 ,其中 表示 最少可以划分成多少个区间,使得每个区间中的元素都是公差为 的等差数列。
答案对输入的 取模, 不一定是质数。
,。
CF1804F Approximate Diameter 做题记录
给你一个边权为 1 的无向图,动态加边,每次加边询问无向图的直径(所有点对的最短路中的最大值)。要求你的答案在真实答案的 21∼2 倍之间(向上取整)。
1≤n,m,q≤105。
CF1556D Take a Guess 做题记录
这是一道交互题,给定两个正整数 n,k,你需要通过 ≤2n 次询问猜出长度为 n 的序列 {ai} 中的第 k 小值。
询问分为两种类型:
or i j,交互器会返回 aioraj 的值。and i j,交互器会返回 aiandaj 的值。其中需要满足 1≤i,j≤n 且 i=j。
最后你需要输出
finish res,其中 res 表示你的答案。3≤n≤104,1≤k≤n,0≤ai≤109。
CF1583D Omkar and the Meaning of Life 做题记录
这是一道交互题。
原来生命的意义是一个 n (2≤n≤100) 的排列。 创造了世上所有生命的 Omkar 知道这个排列,他允许你在有限的询问次数内查询出这个排列是什么。
每一次询问你可以给出一个序列 a1,a2,…,an (1≤a1,a2,…,an≤n) 来对 Omkar 进行询问。 $ a $ 序列不一定要是一个排列。之后 Omkar 会逐个将 ai 与 pi 相加得到一个新的序列 s ,即对于每个 j (1≤j≤n) ,sj=pj+aj 。最后 s 序列中可能会出现一些相同的数,你将读入 Omkar 告诉你的第一个出现相同数的位置。如果没有相同的数出现,你将读入数字 0 。
你最多只能进行 2n 次询问。
CF896B Ithea Plays With Chtholly 做题记录
桌子上面摆着 n 张白纸,交互库会依次给你 m 个 [1,c] 中的数,你每次可以把所获得的数写在一张纸上或者替换掉某一张纸上写的数,在你行动结束后交互库才会给你下一个数。任何时候,如果所有纸上都写了数字并且成非降序排列,你就赢了,直接结束程序。你要想办法赢交互库。
2≤n,m,1≤c≤1000,1≤n⋅⌈2c⌉≤m≤1000。
CF1713D Tournament Countdown 做题记录
这是一道交互题。
有一场由 2n 位选手组成的锦标赛。
这个锦标赛的规则如下:第 1 位选手与第 2 位选手竞争,第 3 位选手与第 4 位选手竞争……以此类推,比赛结束时会只剩下一位参赛选手,这位参赛选手就是胜利者。
你不知道比赛的结果,但你想通过询问评审团来得知最后谁赢了。
每次询问评审团,你需要给定两个正整数 a 和 b,a 和 b 分别代指两位选手的编号。
若 a 选手 比 b 选手 赢的回合更多,评委团将报出数字 1;如果 b 选手 比 a 选手 赢的回合更多,评审团将报出数字 2;如果这两位选手赢的回合一样多,评审团会报出数字 0。
你要做的是在不超过 ⌈31⋅2n+1⌉ 的次数内找到最后胜利的选手。此处 ⌈x⌉ 表示四舍五入 x 到最近的整数。
这场锦标赛已经过去很久了。所以保证有唯一解。
1≤n≤17。
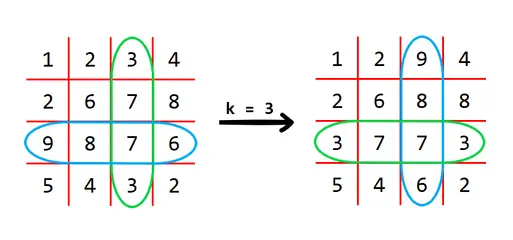
CF1713E Cross Swapping 做题记录
给定一个 n×n 的矩阵。一次操作可以给定一个 k 然后交换所有的 Ai,k 和 Ak,i 。
如图表示 n=4,k=3 的情况。
求若干次操作后字典序最小的矩阵。
1≤n≤1000。
CF1103B Game with modulo 做题记录
未知一个数 a,让你每次猜两个数 x 和 y,若 (xmoda)≥(ymoda) 返回
x,否则返回y。让你猜测次数少于 60 次的时候猜出数 a。1≤a≤109。
CF1088D Ehab and another another xor problem 做题记录
交互题,系统有两个整数 (a,b),你每次可以询问一组整数 (c,d),系统会回答:
- 1 如果 a⊕c>b⊕d
- 0 如果 a⊕c=b⊕d
- −1 如果 a⊕c<b⊕d
其中操作 a⊕b 表示 a 和 b 按位异或。
你需要在询问不超过 62 次之后输出 (a,b) 的值,保证 0≤a,b<230。